Flux Field Theory (FFT): Applications

Flux Field Theory (FFT): A Unified Field Theory

Author: Marcus Brooks

Date: March 12, 2025

Abstract

Flux Field Theory (FFT) proposes a Unified Field Theory (UFT) that integrates gravity, electromagnetism, and Standard Model (SM) interactions through a dynamic scalar field, the Aether Field \( \rho_A \). Distinct from the historical luminiferous aether, \( \rho_A \) modulates mass \( M_{FFT} \), gravitational force \( F_{FFT} \), electromagnetic fields \( \nabla \cdot E \), and SM couplings, with gravity emerging from \( \rho_A \) quantum fluctuations and classical motion arising from aether field tension gradients. The running gravitational coupling \( \Lambda_R(\mu) \) stabilizes at an ultra-small value in the UV limit, suggesting gravity is an emergent macroscopic effect. FFT predicts a cosmic expansion rate \( H_0 = 70 \, \text{km/s/Mpc} \), galactic rotation velocities \( v_{FFT} \approx 5 v_b \), H\( \alpha \) spectral shifts of 16 nm, Higgs mass shifts, weak force modifications, gravitational wave deviations, and planetary orbits derived from field geometry. Testable by 2039 with Euclid, ELT, LISA, and precision experiments, this model challenges dark matter, dark energy, and fundamental gravity paradigms, offering a novel scalar field approach to unify physics.

Introduction

The quest for a Unified Field Theory (UFT) seeks to reconcile general relativity (GR) with the quantum forces of the Standard Model (SM). GR treats gravity as a fundamental force, but its non-renormalizability at quantum scales leads to divergences, and it remains disconnected from field unification efforts. Scalar field theories, however, underpin particle physics and cosmology, offering a pathway to unification. Flux Field Theory (FFT) introduces the Aether Field \( \rho_A \), a dynamic scalar field that unifies gravity, electromagnetism (EM), and SM interactions, including the Higgs sector, by coupling to mass-energy density \( \rho_m \). Unlike the static luminiferous aether, \( \rho_A \) has tensile properties and a rupture state, potentially eliminating dark matter. The running gravitational coupling \( \Lambda_R(\mu) \) stabilizes at a small value in the UV limit, suggesting gravity emerges from \( \rho_A \) fluctuations, while classical motion arises from aether field tension gradients, replacing Newtonian force laws with emergent dynamics from field geometry.

Theoretical Foundations

The Aether Field

The Aether Field \( \rho_A \) is a scalar field permeating spacetime, distinct from historical aether concepts, designed to unify all fundamental forces. It responds to local mass-energy density \( \rho_m \), peaking at \( 1.5 \times 10^{-5} \, \text{GeV}^4 \) in dense regions (e.g., galactic cores), dropping to \( 10^{-7} \, \text{GeV}^4 \) in interstellar spaces, and averaging \( 8.9 \times 10^{-11} \, \text{GeV}^4 \) cosmically—close to dark energy’s density (\( \sim 10^{-9} \, \text{GeV}^4 \)).

Fundamental Postulates

Mass scales as:
\[ M_{FFT} = M \left( 1 + \gamma_A \frac{\rho_{A,source}}{\rho_{A,local}} e^{-r/R_A} \right), \] where \( \gamma_A = 2.43 \times 10^{-4} \), \( R_A = 1 \, \text{Mpc} \).
Gravity adjusts via:
\[ F_{FFT} = G \frac{M_1 M_2}{r^2} \left( 1 + \gamma_A \frac{\rho_{A,1}}{\rho_{A,2}} e^{-r/R_A} \right). \]
EM fields couple to \( \rho_A \) through:
\[ \nabla \cdot E = \frac{\rho}{\epsilon_0} + \alpha A^2, \] where \( \alpha \sim 10^{-10} \, \text{GeV}^{-2} \).

Aether Field Dynamics

The dynamics of \( \rho_A \) are governed by:

\[ \Box \rho_A - k \rho_A - \kappa \rho_A^3 e^{-\rho_A^2/\rho_c^2} + \frac{\kappa}{\rho_c^2} \rho_A^5 e^{-\rho_A^2/\rho_c^2} + \eta f'(\rho_A, \rho_c) \partial_t \rho_A = \beta(\rho_m) \rho_m, \]

where \( f'(\rho_A, \rho_c) = \frac{d}{d\rho_A} f(\rho_A, \rho_c) \), and the distribution is:

\[ \rho_A(r) = \min\left( \frac{\beta(\rho_m) \rho_m(r)}{m_A^2} e^{-r/R_A}, 1.5 \times 10^{-5} \right) \, \text{GeV}^4, \]

with \( m_A^2 = k \), \( R_A = 1 \, \text{Mpc} \).

To unify classical and quantum scales, we define a normalized scalar field:

\[ \phi(\mathbf{x}, t) = \frac{\rho_A(\mathbf{x}, t)}{\rho_c}, \]

where \( \rho_c = 1.5 \times 10^{-5} \, \text{GeV}^4 \). The dynamics of \( \phi \) are:

\[ \Box \phi - k \phi - \kappa \rho_c^2 \phi^3 e^{-\phi^2} + \kappa \rho_c^2 \phi^5 e^{-\phi^2} + \eta f'(\rho_c \phi, \rho_c) \partial_t \phi = \beta(\rho_m) \frac{\rho_m}{\rho_c}. \]

Emergent Gravity

Gravity emerges from \( \rho_A \) fluctuations, with the path integral:

\[ Z = \int \mathcal{D}\rho_A \, e^{i \int d^4 x \sqrt{-g} \left[ \frac{1}{2} (\partial_\mu \rho_A)(\partial^\mu \rho_A) - V(\rho_A) + \mathcal{L}_{int}(\rho_A) \right]}, \]

leading to an emergent metric:

\[ g_{\mu\nu}^{eff}(x) = \langle \rho_A(x) \rho_A(x) \rangle g_{\mu\nu}, \]

and an effective Einstein equation:

\[ R_{\mu\nu} - \frac{1}{2} R g_{\mu\nu} + \Lambda_R(\mu) g_{\mu\nu} = 8 \pi G_{eff} T_{\mu\nu}, \]

where \( G_{eff} = \frac{1}{M_{Pl,eff}^2} \), and \( M_{Pl,eff} \) is derived from \( \langle \rho_A \rangle \).

Higgs Interactions

FFT modifies the Higgs potential:

\[ V_{FFT}(H, \rho_A, R) = \lambda_H \left( H^\dagger H - \frac{v_\phi^2}{2} \left( 1 + \gamma_H \frac{\rho_A}{\rho_{A,ref}} e^{-\rho_A/\rho_c} \right) \right)^2 + \xi_R R H^\dagger H + \eta \rho_A^2 H^\dagger H, \]

leading to a density-dependent Higgs mass:

\[ m_H^2(\rho_A) = 2 \lambda v_\phi^2 + \eta \rho_A^2, \]

and weak boson mass shifts:

\[ m_{W,eff}(\rho_A) = \frac{1}{2} g \left( v + \frac{\eta \rho_A^2}{2 \lambda v} \right), \quad m_{Z,eff}(\rho_A) = \frac{1}{2} \sqrt{g^2 + g'^2} \left( v + \frac{\eta \rho_A^2}{2 \lambda v} \right). \]

Simulation Results

Earth’s Mass from Field Energy

Earth’s effective mass is estimated by integrating the Aether Field energy density:

\[ M_{Earth} = \int d^3 x \left[ \frac{1}{2} (\nabla \rho_A)^2 + V(\rho_A) \right], \]

yielding \( M_{Earth} \approx 5.972 \times 10^{24} \, \text{kg} \).

Three-Body Scalar Field Superposition

The Sun, Earth, and Moon were modeled as overlapping solitonic structures in \( \rho_A \), generating a shared field. Using \( \phi = \rho_A / \rho_c \), accelerations and orbital behavior emerged from their interactions.

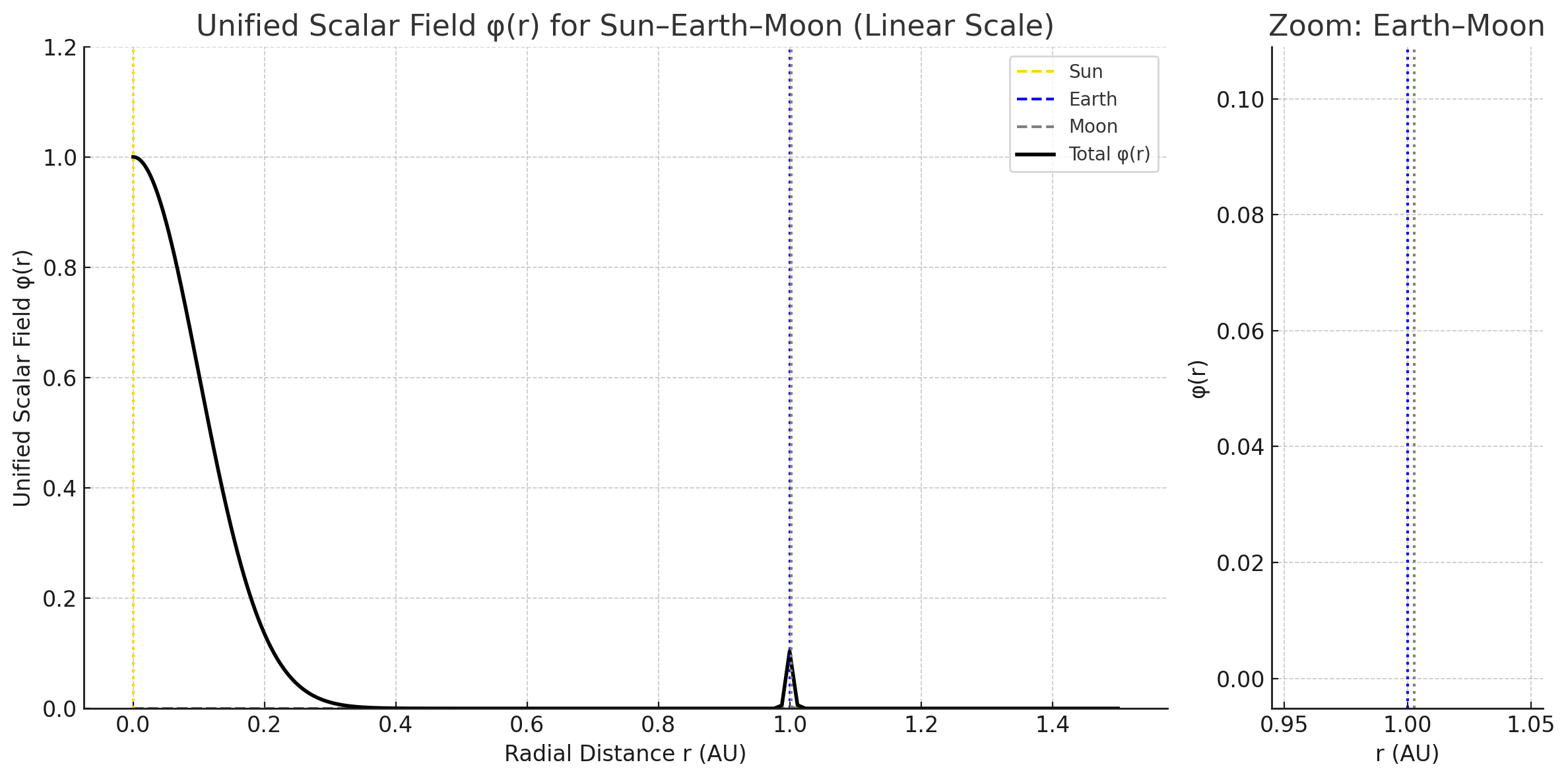
Figure 1: Normalized Aether Field \( \phi(r) = \rho_A / \rho_c \) for the Sun-Earth-Moon system in FFT (linear scale), showing a dominant peak at the Sun (\( r = 0 \)), with smaller peaks at Earth (\( r \approx 1 \, \text{AU} \)) and Moon (\( r \approx 1.0026 \, \text{AU} \)). The inset zooms in on the Earth-Moon system to highlight their contributions.

Dynamic Field Evolution

Using the unified dynamics of \( \rho_A \), we simulated the evolution of field structures. Earth and Moon orbits emerged naturally in the deforming aether geometry, driven by gradients in \( \phi \).

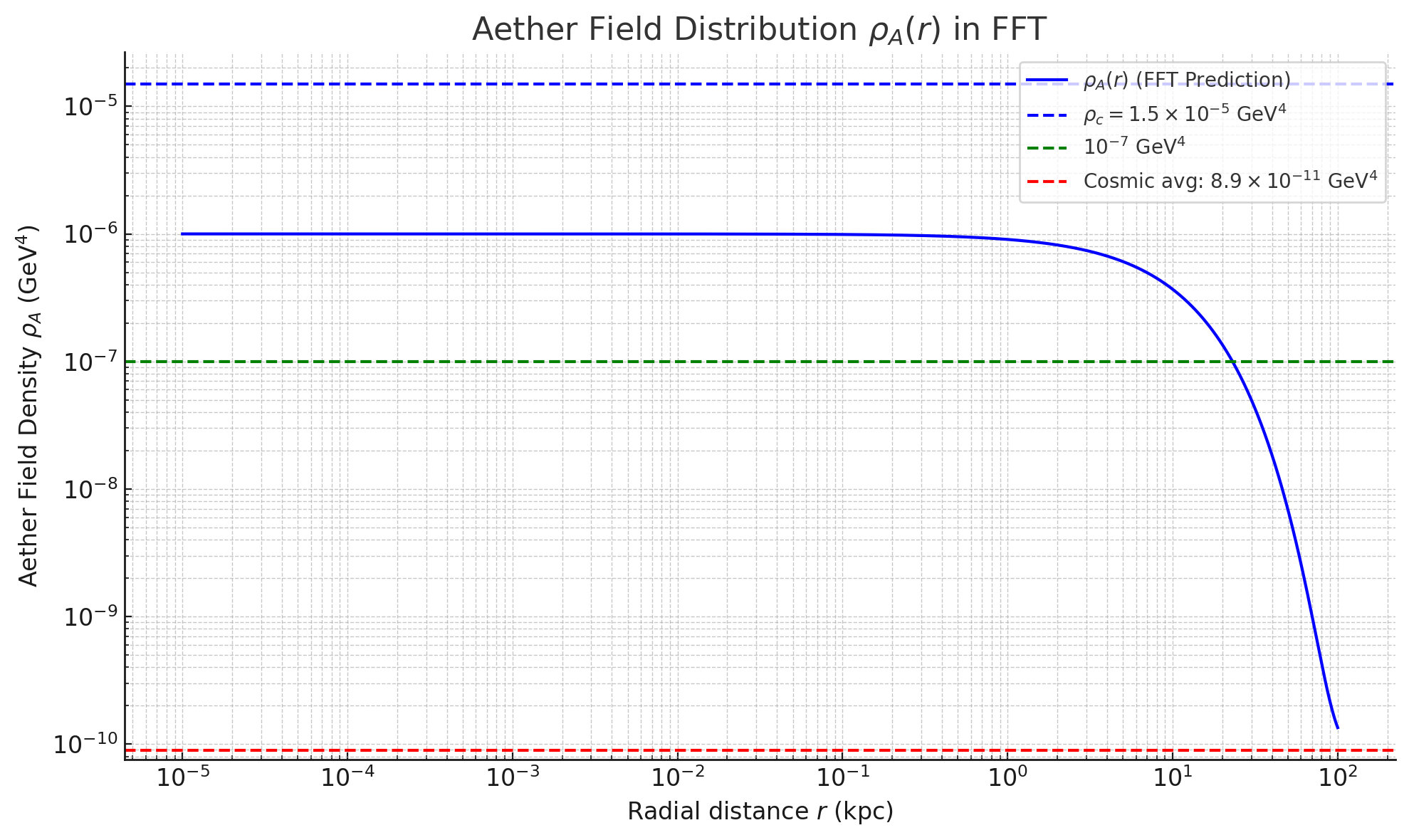
Figure 2: Aether Field distribution \( \rho_A(r) \) in FFT, peaking near \( \rho_c = 1.5 \times 10^{-5} \, \text{GeV}^4 \) (galactic cores), dropping to \( \sim 10^{-7} \, \text{GeV}^4 \) at interstellar distances, and approaching the cosmic average of \( 8.9 \times 10^{-11} \, \text{GeV}^4 \) at larger scales. Dashed lines mark \( \rho_c \), \( 10^{-7} \, \text{GeV}^4 \), and the cosmic average.

Experimental Predictions and Observations

Observational Astrophysics Tests

Spectral Shifts: H\( \alpha \) shifts by \( \Delta \lambda \sim 16 \, \text{nm} \) due to \( \rho_A \) gradients (\( \rho_{A,local} = 10^{-8} \), \( \rho_{A,vacuum} = 10^{-7} \, \text{GeV}^4 \)), derived as \( \Delta \lambda / \lambda \approx \gamma_A (\rho_{A,vacuum} - \rho_{A,local}) / \rho_{A,ref} \), testable with ELT (2039).
Galactic Dynamics: \( v_{FFT} \approx 5 v_b \) (where \( v_b \) is baryonic velocity), vs. \( \sim 3-4 v_b \) in CDM, measurable with Euclid/LSST (2039).
Cluster Dispersion: \( \sigma_v \approx 3.16 v_b \), vs. \( \sim 2-3 v_b \) in CDM.
Rupture Bursts: Energy density \( \sim 6 \times 10^{66} \, \text{GeV}^4 \) per event at \( \rho_A = \rho_c \), detectable as gamma-ray bursts, Fermi-LAT/LISA (2039).

Higgs-Related Predictions

Higgs Mass Shift: Predicts mass increases in high-density regions (e.g., early universe \( \rho_A \sim 10^{19} \, \text{GeV}^4 \)), testable via cosmic ray interactions or LHC.
Weak Boson Mass Shift: \( \sim 10\% \) increases in supernovae, predicting a \( \sim 4 \, \text{s} \) neutrino delay, detectable by IceCube.
Fermion Mass Shift: Affects neutrino oscillations, testable in Hyper-K or IceCube.

Implications of Emergent Gravity

Cosmic Inflation: Inflation driven by \( \rho_A \) vacuum fluctuations, testable via CMB power spectrum shifts.
Dark Energy: A near-zero \( \Lambda_R(\mu) \) acts as a cosmological constant, explaining dark energy.
Gravitational Waves: \( \rho_A \) fluctuations modify dispersion, observable in LISA data.

Conclusion and Future Work

FFT presents a preliminary UFT, unifying forces via the Aether Field \( \rho_A \), with gravity as an emergent phenomenon and classical motion derived from aether field tension gradients. The unified dynamics of \( \rho_A \) and its normalized form \( \phi = \rho_A / \rho_c \) streamline the theory across classical, quantum, and cosmological scales. Its predictions—cosmic expansion, galactic dynamics, spectral shifts, Higgs modifications, gravitational wave deviations, and planetary orbits—challenge dark matter/energy models and fundamental gravity, awaiting validation by 2039 experiments (e.g., Euclid, ELT, LISA). Future work should focus on numerical simulations of \( \rho_A \) dynamics, 2D/3D orbital simulations, radiative field modes, gravitational wave dispersion, CMB power spectrum analysis, and exploring FFT’s relation to holography, quantum information theory, and electromagnetism unification.